前編では基本的なグラフについて紹介してきました。後編で紹介する4種類のグラフは統計的な考え方も用いたグラフ表現です。
散布図
散布図は2変数間の関係性を把握したいときに、絶大な効果を発揮する可視化方法です。縦軸と横軸にそれぞれの変数の量をとり、2軸の座標上にプロットします。つまり、一方の変数の値の増減が、もう一方の変数の値にどのように関係するのか一目でわかります。これによって、変数間の関係性が明らかになるというわけです。例えば、気温と売り上げ数量の関係性を知りたいと思った時に、下記のように散布図で可視化すると、その関係性が明らかとなります。

上記の場合は気温が上昇すると売り上げ数量も上がっていく関係性があると見て取れます。2変数の関係性については相関係数という指標を求めて把握することも多いですが、散布図で表すと視覚的に把握することができるため、手早く実施したい場合にはおすすめな手法です。
箱ひげ図
箱ひげ図は複数変数間のデータのばらつき具合を可視化するために用います。基本統計量の算出について以前、説明しましたが、それらを可視化するための手段として箱ひげ図はよく用いられています。MicrosoftのExcelにはテンプレートで箱ひげ図を作成できませんので、イメージはオープンソースの統計解析システム 「R」を用いた箱ひげ図を使っています。
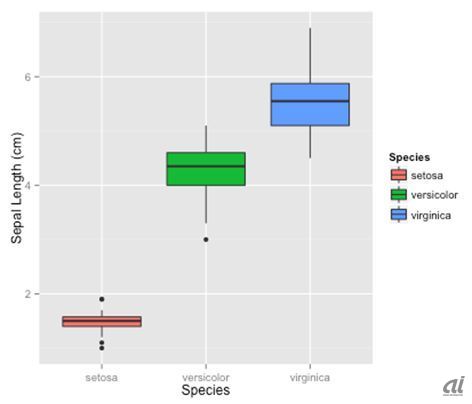
Rに搭載されているデータで最もよく使用されるirisデータ(あやめ)を箱ひげ図で可視化しました。setosa、versicolor、virginicaという3品種の「がく片」の長さのばらつき具合がこれで一目瞭然です。ひげの両端がそれぞれ最大値、最小値です。ひげよりも外にある点は外れ値としてプロットされています。
箱の両端がそれぞれ第3四分位(全体を等分した際の75%)、第1四分位(全体を等分した際の25%)、箱の中の線が中央値を表していることで、観測データがどのようにばらついているか、他の変数と比較してどうちらばっているかを検討します。






