今日からできるスパースモデリング
連載第2回目では実践編といこう。スパースモデリングを駆使することで、データからの本質部分を抽出することができるということを第1回で紹介した。さらにさまざまな要因でデータの取得量が制限されてしまう場合に、少量のデータからでも、その性質を生かして満足のいく精度で知見を得ることが可能であることを説明した。
スパースモデリングの言葉と物語を知るだけではなく、その威力を実際に試し、「あのデータを使って面白いことができないだろうか」と考えを巡らせてもらいたい。もちろん目的によって、どんな解析手段が適するかは変わってくる。しかし、その根底となるやり方は共通しているというのがスパースモデリングの強みである。今回はその基本部分を紹介することで、更なる追求の出発点にしよう。
従来のデータ追従型の解析法
実験的にある入力をしたときに、出力が得られたとする。このときにこの入力と出力のセットもいくつか得られた。どうもこれは何かの法則に従っているように思う。その背後にある法則を知りたい(「ビールとおむつが一緒に売れる」のようなデータを法則に落とし込むことこそ、ビジネスの現場で必要だ)。例えば前回あげたフックの法則などがその典型例だ。バネにつけたおもりを増やしていくと、バネの長さが伸びる。このときにバネについけたおもりの個数とバネの長さの関係を知りたいとする。
それでは表1のようにデータが得られたとしよう。図1のようにグラフに示すと、直線の関係がありそうだな、と見当がつく。それぞれの点に合うように画面にボールペンをかざして探ってみたくなる。これはいわゆる直線によるフィッティング、回帰問題と呼ばれるものである。これはさまざまな直線を当てはめて、どんな傾きが良いか、どんな切片(グラフと座標軸の交点)が良いかを探り、最適なものを選択することに対応している。
| X(おもりの個数) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Y(バネの長さ) | 7.0598 | 9.2578 | 11.6488 | 13.7823 | 15.9804 |
さて皆さんは、人間だ。機械とは違う。柔軟にボールペンをかざして、何となく気に食わないからと傾けたり、上下左右に動かしたりして、どの点にも近い直線を見つけることが何となくできる。点と直線がちょっとズレて、気に食わないなあと思うかもしれない。このズレの大きさを最も小さくなるようにする計算方法を「最小二乗法」と呼ぶ。
観測データに対して最も近い数式を求めるには、この観測値と平均の差を最小化した計算式が有効であり、「回帰分析」を利用できるため、これまでのデータ解析の基本として利用されてきた。いわば既存の概念の代表格といえる。この人間ができることを代わりにさせるというのが機械学習の発想の基本であり、データ解析の現場で行われていることだ。
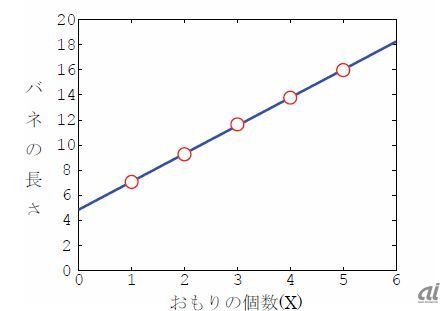
図1:バネの長さ(Y)とおもりの個数(X)の関係