前回、オープンソースの統計解析ソフト「R」の簡単な使い方を説明しました。今回は、実際にRにあるデータセットを使い、回帰分析に取り組み、その結果をどのように使っていくかを説明したいと思います。
回帰分析とは
回帰分析とは、「目的変数」と「説明変数」間の関係を表す式を統計的な手法によって推計する分析のことです。
目的変数とは予測の対象とする「量」のことであり、説明変数は目的変数を説明、つまり物事の原因を表すのに使う変数です。この2つの変数にどんな関係があるのか、例えば天候という変数は、売り上げにどう影響するかを数式で表すために回帰分析を使います。
今回の記事についての回帰分析は特に断りがない場合、すべて線形回帰分析、つまり「直線をモデル」に複数の変数間の相関を説明しようとする分析手法のことを指します。
言葉で説明してもピンと来ない方も多いと思いますので、最も単純な例を挙げましょう。下記は1つの変数である目的変数を説明した場合の単回帰分析の関係式の例です。

上記のyが先ほど定義した目的変数、xが説明変数です。この関係式を用いてa,bの値を推定し、関係式を作り上げることが回帰分析です。
もう少し具体的にイメージしてもらうために、身近な事例を考えてみましょう。
下記は身長のデータから体重を説明することができるかを散布図で表したものです。
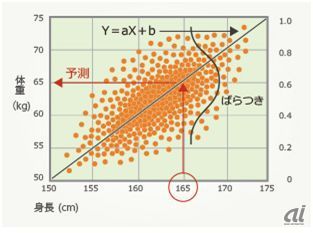
(ALBERTより画像提供)
つまり、a(傾き)とb(切片)がわかれば、X(身長)からY(体重)を説明することができるわけです。では、実際にどのようにしてa、bの値を推測するのでしょうか。
誌面の都合上詳細な説明は割愛しますが、「最小二乗法」を行うことができるのが、回帰分析です。
最小二乗法は得られた数値を、想定した関数に対して最も近い値に残差(測定値と平均の差)の二乗和(各数字をすべて2乗して足す)を最小化する方法です。観測データに対して最も近しい数式を求めるのには、この観測値と平均の差を最小化したものがよいのです。
この身長と体重のグラフでは、2つの関係を表す数式を求めたいという場合、(何も考えなければ)データの中にいかようにも線を引くことができます。
それだと数式を導き出しても当てはまりがよくないため、何かしらの基準を設ける必要があります。最小二乗法で観測されたデータの平均を基準として、各データからの差(これが残差)を最小化した数式がデータから得られた数式として最もよいものだろうということです。
測定誤差があるデータを、直線のグラフにして理解しやすくする方法と考えるとわかりやすいでしょうか。
このように目的変数と説明変数の関係性を数式で示せれば、目標に対して、再現性の高い施策をうてる可能性が高いのです。
また、説明変数が2つ以上に増える場合は重回帰分析と呼ばれます。実務で多く使われるのが、この重回帰分析です。





